Movimiento rectilíneo uniformemente variado, MRUV
Se trata de un tipo de movimiento muy característico, que además de sencillo, aparece bastante seguido en la naturaleza. Su nombre lo caracteriza: la palabra rectilíneo indica que la trayectoria coincide con una recta; y la palabra variado alude a la velocidad, que ya no es constante... pero que varía uniformemente . Ojo: la velocidad -ahora variable- ya no se puede homologar a la velocidad media. Mirá el esquema: en tiempos iguales, aumentos iguales de velocidad. Los desplazamientos ya no son iguales, dado que a mayor velocidad, tendremos mayores desplazamientos. | ||||||
 | ||||||
| La flecha de abajo del ciclista representa la velocidad. Un gráfico velocidad-tiempo típico de un MRUV podría ser el siguiente: | ||||||
| ||||||
| Si la recta fuese horizontal representaría un móvil que no cambia la velocidad, y en ese caso se trataría de un MRU. Aunque parezca ridículo también lo incluimos dentro de los MRUV. La orientación prohibida es la vertical: indicaría que el móvil posee infinitas velocidades en un mismo instante. Fijate que la recta no necesariamente pasa por la posición v = 0 en el instante v = vo + a ( t – to )v y t son las variables. Si no aparecen, fuiste; no hay ecuación horaria. El resto: vo , a y to , son constantes, o sea números. vo y to son una velocidad cualquiera que el móvil tenga y el instante en que la haya tenido (o sea, se corresponden entre sí). Y a es la magnitud que describe el cambio de velocidad y se llama aceleración. Justamente, la característica fundamental del MRUV es a = cte. Gracias a eso, podemos calcularla como una aceleración media, am. | las unidades de la aceleración son m/s²o cualquier otra unidad de longitud sobre cualquier unidad de tiempo al cuadrado | |||||
miércoles, 19 de febrero de 2014
Movimiento rectilíneo Uniformemente Variado (Información).
Mas teoria MRUV
Aceleración en MRUV
El MRUV es un movimiento en el cual un móvil se desplaza en línea recta a una velocidad que varía de manera uniforme a lo largo del tiempo. Esta velocidad puede aumentar (y en ese caso el movimiento es acelerado) o disminuir (desacelerado). Al variar la velocidad en el tiempo, en tiempos iguales recorre distancias distintas. La aceleración tiene un valor distinto de cero (positivo o negativo). El espacio varía con el cuadrado del tiempo.La tasa de variación de la velocidad se denomina aceleración. Su valor puede ser positivo o negativo. La aceleración es una magnitud vectorial con lo cual, además de un módulo, tenemos una dirección y un sentido.
Un signo negativo en la aceleración no necesariamente significa que la velocidad esté disminuyendo en valor absoluto. Puede estar aumentando en el sentido contrario al positivo del sistema de referencia fijado.
Si la velocidad viene disminuyendo y se hace cero sin que cambie la aceleración, el móvil se detendrá y comenzará a moverse en sentido contrario, esta vez aumentando su velocidad en valor absoluto. El vector que sí cambia de signo es el de la velocidad cuando comienza a moverse para el otro lado, pero la aceleración en este caso será la misma.
Signo de la aceleración
Si el móvil tiene velocidad de signo positivo y aumentando, la aceleración es positiva.Si el móvil tiene velocidad de signo positivo y disminuyendo, la aceleración es negativa. Es decir que disminuye la velocidad hasta que se haga cero. Luego, con esta misma aceleración negativa, el móvil comenzará aumentar de velocidad (en módulo) pero con signo negativo.
Si el móvil tiene velocidad negativa y aumentando, la aceleración es negativa. La velocidad aumenta pero con en el signo contrario al sistema. Si el móvil se estaba moviendo antes de comenzar a contar el tiempo, en algún momento la velocidad podría haber sido cero (antes de ser negativa) y antes de eso positiva en disminución.
Si el móvil tiene velocidad negativa y disminuyendo, la aceleración es positiva. El móvil en algún momento se detendrá y comenzará a aumentar la velocidad en el sentido positivo (primer caso).
Valor de la aceleración
El valor de la aceleración se calcula como la variación de la velocidad en un tiempo determinado.
La aceleración se mide en metros sobre segundos al cuadrado.
Gráficos de ejemplo
Gráfico de la aceleración respecto del tiempo en el movimiento rectilíneo uniformemente variado.

domingo, 16 de febrero de 2014
viernes, 14 de febrero de 2014
Movimiento rectilíneo Uniformememente Variado
Movimiento Rectilíneo Uniformemente Variado:
- Movimiento: Un cuerpo esta en movimiento cuando suposición varia con el tiempo con respecto a un punto que se considera fijo.
*Rectilíneo: La trayectoria es una línea recta y el módulo de la velocidad varía proporcionalmente al tiempo.
Este movimiento puede ser acelerado si el modulo de la velocidad aumenta a medida que transcurre el tiempo y retardado si el modulo de la velocidad disminuye el transcurso del tiempo.
Conceptos básicos que hay que tener claros, necesarios para el movimiento uniformemente variado
(ELEMENTOS del M.U.V.):
- Móvil: Es todo cuerpo que es capaz de moverse.
- Trayectoria: Es la línea que describe un cuerpo es su desplazamiento.
- Velocidad: Es la variación de la posición de un cuerpo por unidad de tiempo.
- Velocidad-Media: Es la velocidad constante que hubiera tenido que llevar el móvil para recorrer la misma distancia y en el tiempo en que lo hizo con movimiento variado.
- Velocidad-Instantánea: Es la velocidad media en un intervalo muy corto.
- Aceleración: Es la variación que experimenta la rapidez por unidad de tiempo.
- Tiempo máximo: Es el tiempo que trascurre desde el momento en que un móvil inicia un movimiento uniformemente retardado, hasta que detiene.
- Desplazamiento máximo: Es el desplazamiento alcanzado por un móvil desde el momento que se inicia el
miércoles, 12 de febrero de 2014
MRU
Movimiento rectilíneo
Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.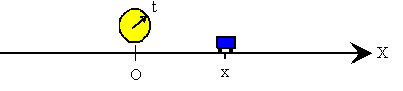
En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.
Posición
La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t).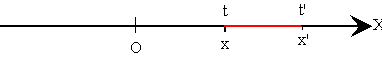
Desplazamiento
Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Dx=x'-x en el intervalo de tiempo Dt=t'-t, medido desde el instante t al instante t'.
Velocidad
La velocidad media entre los instantes t y t' está definida porPara determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Dt tan pequeño como sea posible, en el límite cuando Dt tiende a cero.
Pero dicho límite, es la definición de derivada de x con respecto del tiempo t.
Para comprender mejor el concepto de velocidad media, resolvemos el siguiente ejercicio
Ejercicio
Una partícula se mueve a lo largo del eje X, de manera que su posición en cualquier instante t está dada por x=5·t2+1, donde x se expresa en metros y t en segundos.
Calcular su velocidad promedio en el intervalo de tiempo entre:
- 2 y 3 s.
- 2 y 2.1 s.
- 2 y 2.01 s.
- 2 y 2.001 s.
- 2 y 2.0001 s.
- Calcula la velocidad en el instante t=2 s.
En el instante t=2 s, x=21 m
| ||||
t’ (s)
|
x’ (m)
|
Δx=x'-x
|
Δt=t'-t
| |
3
|
46
|
25
|
1
|
25
|
2.1
|
23.05
|
2.05
|
0.1
|
20.5
|
2.01
|
21.2005
|
0.2005
|
0.01
|
20.05
|
2.001
|
21.020005
|
0.020005
|
0.001
|
20.005
|
2.0001
|
21.00200005
|
0.00200005
|
0.0001
|
20.0005
|
...
|
...
|
...
|
...
|
...
|
0
|
20
| |||
Como podemos apreciar en la tabla, cuando el intervalo Δt→0, la velocidad media tiende a 20 m/s. La velocidad en el instante t=2 s es una velocidad media calculada en un intervalo de tiempo que tiende a cero.
Calculamos la velocidad en cualquier instante t
- La posición del móvil en el instante t es x=5t2+1
- La posición del móvil en el instante t+Dt es x'=5(t+Dt)2+1=5t2+10tDt+5Dt2+1
- El desplazamiento es Dx=x'-x=10tDt+5Dt2
- La velocidad media <v> es
La velocidad en el instante t es el límite de la velocidad media cuando el intervalo de tiempo tiende a cero
La velocidad en un instante t se puede calcular directamente, hallando la derivada de la posición x respecto del tiempo.
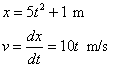
En el instante t=2 s, v=20 m/s
Aceleración
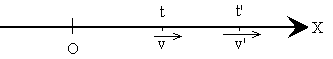
En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante t la velocidad del móvil es v, y en el instante t' la velocidad del móvil es v'. Se denomina aceleración media entre los instantes t y t' al cociente entre el cambio de velocidad Dv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Dt=t'-t.
La aceleración en el instante t es el límite de la aceleración media cuando el intervalo Dt tiende a cero, que es la definición de la derivada de v.
Ejemplo:
Un cuerpo se mueve a lo largo de una línea recta x=2t3-4t2+5 m. Hallar la expresión de
- La velocidad
- La aceleración del móvil en función del tiempo.
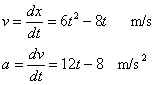
Dada la velocidad del móvil hallar el desplazamiento
Si conocemos un registro de la velocidad podemos calcular el desplazamiento x-x0 del móvil entre los instantes t0 y t, mediante la integral definida.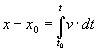
El producto v dt representa el desplazamiento del móvil entre los instantes t y t+dt, o en el intervalo dt. El desplazamiento total es la suma de los infinitos desplazamientos infinitesimales entre los instantes t0 y t.
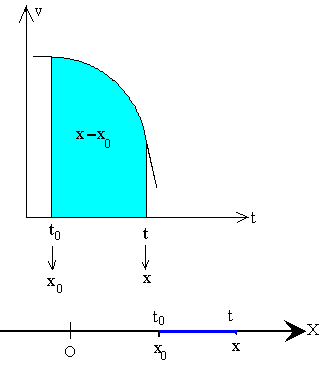 | En la figura, se muestra una gráfica de la velocidad en función del tiempo, el área en color azul mide el desplazamiento total del móvil entre los instantes t0 y t, el segmento en color azul marcado en la trayectoria recta.Hallamos la posición x del móvil en el instante t, sumando la posición inicial x0 al desplazamiento, calculado mediante la medida del área bajo la curva v-t o mediante cálculo de la integral definida en la fórmula anterior. |
Ejemplo:
Un cuerpo se mueve a lo largo de una línea recta de acuerdo a la ley v=t3-4t2 +5 m/s. Si en el instante t0=2 s. está situado en x0=4 m del origen. Calcular la posición x del móvil en cualquier instante.
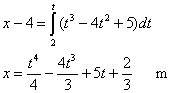
Dada la aceleración del móvil hallar el cambio de velocidad
Del mismo modo, que hemos calculado el desplazamiento del móvil entre los instantes t0 y t, a partir de un registro de la velocidad v en función del tiempo t, podemos calcular el cambio de velocidad v-v0 que experimenta el móvil entre dichos instantes, a partir de un registro de la aceleración en función del tiempo.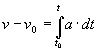
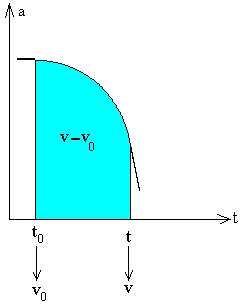 | En la figura, el cambio de velocidad v-v0 es el área bajo la curva a-t, o el valor numérico de la integral definida en la fórmula anterior.Conociendo el cambio de velocidad v-v0, y el valor inicial v0 en el instante t0, podemos calcular la velocidad v en el instante t. |
La aceleración de un cuerpo que se mueve a lo largo de una línea recta viene dada por la expresión. a=4-t2 m/s2. Sabiendo que en el instante t0=3 s, la velocidad del móvil vale v0=2 m/s. Determinar la expresión de la velocidad del móvil en cualquier instante
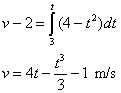
Resumiendo, las fórmulas empleadas para resolver problemas de movimiento rectilíneo son
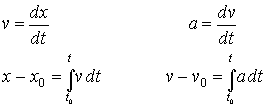
Movimiento rectilíneo uniforme
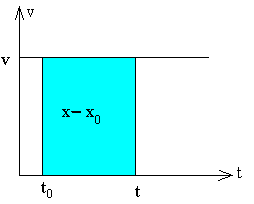 | Un movimiento rectilíneo uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero. La posición x del móvil en el instante t lo podemos calcular integrando o gráficamente, en la representación de v en función de t. |
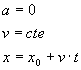
Suscribirse a:
Entradas (Atom)









